
Transformada Z
"La Transformada Z: una herramienta poderosa para analizar señales discretas"
Introduccion
La transformada de Fourier juega un rol clave en la representación y el análisis de señales y sistemas discretos. Ahora vamos a utilizar una generalización de la transformada de Fourier que se conoce como transformada z. La transformada z es para señales discretas lo que la transformada de Laplace es a las señales continuas, y ambas tienen una relación similar a su correspondiente transformada de Fourier. Una motivación para esta generalización es que la transformada de Fourier no converge para todas las secuencias, y seria útil una generalización de ella que abarque una mayor cantidad de señales.
Transformada Z
La transformada de Fourier X(e^jw) de una secuencia x[n] se define como:
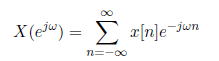
La transformada-z X(z) de una secuencia x[n] se define como:
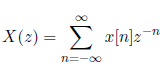
z es una variable compleja, z = re^jw. Cuando r = 1, X(z) = X(ej!). Algunas veces se considera que la transformada z es un operador que transforma una secuencia en una función. Con esta interpretación, la secuencia x[n] se convierte en la función X(z), donde z es una variable compleja continua. La transformada z que hemos definido se conoce como bilateral. La transformada z unilateral se define como:
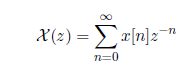
Estas transformadas
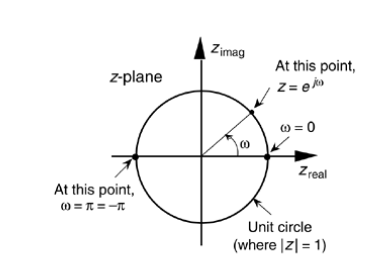
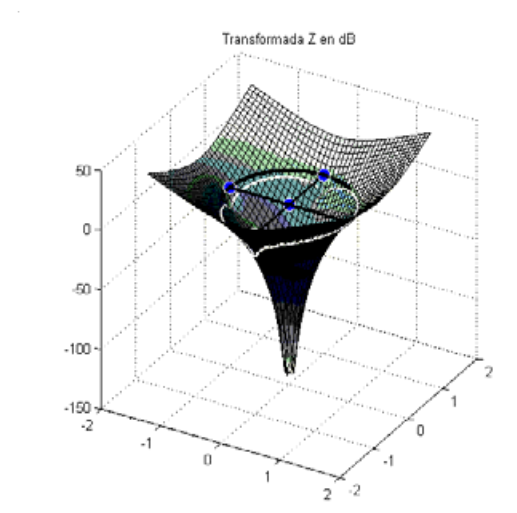
Note que "w" es el ángulo entre el vector asociado a un punto z en el círculo unitario y el eje real del plano complejo z. Si evaluamos X(z) en puntos del círculo unitario comenzando en z = 1(w= 0) hasta z = -1(w = π), obtenemos la transformada de Fourier de 0 <= w <= π. Si continuamos evaluando X(z) alrededor del círculo unitario eso correspondería a obtener la transformada de Fourier de w = π hasta w = 2π . Con esta interpretación, la periodicidad en frecuencia de la transformada de Fourier es capturada naturalmente.
Region de Convergencia
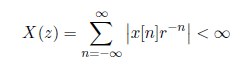
para la convergencia de la transformada Z. Dada la ecuación anterior, debido a la multiplicación de la secuencia por el exponencial real r^-n es posible que la transformada Z converga aunque no lo haga la transformada de Fourier. La convergencia de la transformada Z depende de |z|, ya que como |X(z)| < ∞ si:
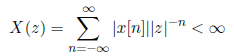
la ROC de la transformada Z consiste de todos los valores de z para lo que la desigualdad anterior se cumple. Entonces, si un valor z, digamos z1, se encuentra en la ROC, entonces todos los valores de z en el círculo definido por |z| = |z1| estarán también en la ROC. Como consecuencia de esto, la ROC consistirá de un anillo en el plano z centrado alrededor del origen. Su límite superior será un círculo (o se extenderá al infinito), y su límite inferior sera un círculo (o se extenderá hasta el origen). Si la ROC incluye el círculo unitario, la transformada de Fourier de la secuencia converge.
Las series de potencias de la transformada Z son series de Laurent, por lo que muchos teoremas de variable compleja se utilizan en el estudio de la transformada Z. Una serie de Laurent representa una función analítica en cada punto del interior de la región de convergencia, por lo que la transformada z y todas sus derivadas con respecto a "w" deben ser funciones continuas de "w". La transformada z es muy útil cuando se expresa en forma cerrada, pero también lo es cuando se expresa como una función racional:
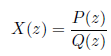
donde P(z) y Q(z) son polinomios de z. Los valores de z para los cuales P(z) = 0 se denominan ceros de X(z), y los valores de z para los cuales Q(z) = 0 se denominan polos de X(z).
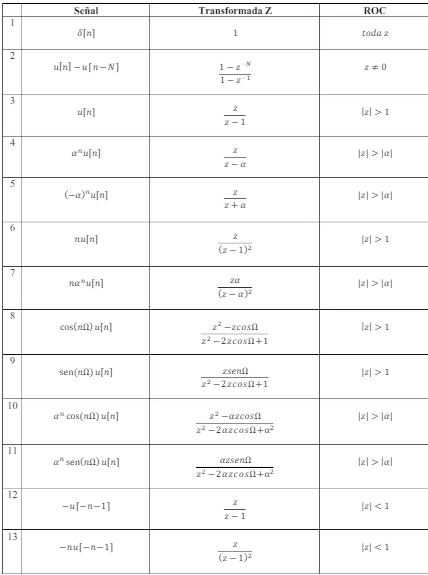
Propiedade de la Region de Convergencia
1. La ROC es un disco o un anillo centrado en el origen del plano Z.
2. La transformada de Fourier de x[n] converge si y sólo si la ROC de la transformada z de x[n] incluye al círculo unitario.
3. La ROC no puede contener polos.
4. Si x[n] es de duración finita, la ROC se extiende en todo el plano Z hasta el in nito, excepto posiblemente z = 0 o z = ∞ .
5. Si x[n] es una secuencia del lado derecho, la ROC se extiende desde el polo más externo hasta el infinito.
6. Si x[n] es una secuencia del lado izquierdo, la ROC se extiende desde el polo más interior hacia el origen.
Propiedades de la Transformada Z
Algunas propiedades importantes de la transformada Z incluyen:

Aplicaciones de la Transformada Z
- Análisis de sistemas lineales e invariantes en el tiempo (LTI): Permite analizar la respuesta de sistemas LTI discretos.
- Diseño de filtros digitales: Facilita el diseño y análisis de filtros digitales.
- Estabilidad de sistemas discretos: Ayuda a determinar la estabilidad de un sistema mediante la ubicación de los polos en el plano Z.
Bibliografia
Oppenheim, A. V., Schafer, R. W., & Buck, J. R. (1999). Discrete-Time Signal Processing (2nd ed.). Prentice Hall.
Proakis, J. G., & Manolakis, D. G. (2007). Digital Signal Processing: Principles, Algorithms, and Applications (4th ed.). Pearson Prentice Hall.
Nuestro equipo

Eduardo Mercado Hernandez
Creador de contenido